Estimating the size of a safe minimal cubic PBC box for a peptide folding simulation
Beware. What follows is primitive and possibly plain wrong.
The idea is this : can we safely reduce the size of the cell for a folding simulation ? The word 'safely' in the previous sentence must be understood in a probabilistic sense : we want the smallest cubic cell for which the probability of neighboring peptide images interacting with each other (due to PBC) is less than an arbitrarily set threshold. What follows is an attempt to do just that.
Assuming an ideal chain and using the equations from this page we have :
The average end-to-end distance is 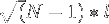 where
where 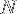 is the number of amino acids and
is the number of amino acids and 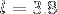 is the average
is the average  distance.
distance.
The variance of this end-to-end distance along any of the orthogonal axes is 
If we require that the edge of the (cubic) PBC box must be longer than at least  plus this average end-to-end distance, then the minimal box size
plus this average end-to-end distance, then the minimal box size 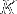 is given by
is given by
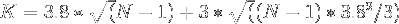
which reduces to
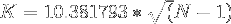
Applying the above equation gives the following estimates :
| Number of peptide residues | Estimated minimal cubic PBC cell edge length (Å) |
|---|---|
| 10 | 31.2 |
| 12 | 34.5 |
| 14 | 37.4 |
| 16 | 40.2 |
| 18 | 42.8 |
| 20 | 45.2 |
| 22 | 47.6 |
| 24 | 49.8 |
| 26 | 51.9 |
| 28 | 54.0 |
| 30 | 55.9 |
| 32 | 57.8 |
| 34 | 59.6 |
| 36 | 61.4 |







